Algorithms Throw Back
I was given a question today that really took me back. Here’s a hint: it had to do with binary search trees, data structures, and pretty printing.
I haven’t touched a BST in six years so it took some priming to get me going.
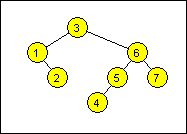
The task was to print this tree level by level. So the output should be 3, 1, 6, 2, 5, 7, 4. If you’re a programmer, I encourage you to solve this problem as an exercise before looking at my solution. It was humbling for me.
After wasting a half hour messing around with recursion, I was given a pretty nice hint to do it iteratively with a queue.
I still failed miserably with my good old paper and pencil, but afterwards set out to do it in a more comfortable environment (C#).
Here’s my basic node class (structs are for sissys):
public class Node
{
public Node(int value, Node left = null, Node right = null)
{
Value = value; Left = left; Right = right;
}
public int Value { get; set; }
public Node Left { get; set; }
public Node Right { get; set; }
}
And my main program:
static void Main(string[] args)
{
Node n = new Node(3);
n.Left = new Node(1, null, new Node(2));
n.Right = new Node(6, new Node(5, new Node(4)), new Node(7));
PrettyPrintByLevel(n);
Console.ReadKey();
}
And the magic:
static void PrettyPrintByLevel(Node n)
{
Queue<Node> Nodes = new Queue<Node>();
Nodes.Enqueue(n);
do
{
Node QNode = Nodes.Dequeue();
Console.WriteLine(QNode.Value);
if (QNode.Left != null) Nodes.Enqueue(QNode.Left);
if (QNode.Right != null) Nodes.Enqueue(QNode.Right);
} while (Nodes.Count > 0);
}
A quick test reveals that it works:
3 1 6 2 5 7 4
Yay! So what did I learn today? I’m rusty on the basics and need to do some more Project Euler problems.
I’ve taken this opportunity to brush up on some Java. Here’s the same app in the similar, but different Java:
public static void main(String[] args) {
// build up a tree
Node n = new Node(3, null, null);
n.Left = new Node(1, null, new Node(2, null, null));
n.Right = new Node(6, new Node(5, new Node(4, null, null), null), new Node(7, null, null));
// print out the tree to the console
PrettyPrintByLevel(n);
}
private static void PrettyPrintByLevel(Node n) {
Queue<Node> Nodes = new LinkedList<Node>();
Nodes.add(n);
do
{
Node QNode = Nodes.remove();
System.out.println(QNode.Value);
if (QNode.Left != null) Nodes.add(QNode.Left);
if (QNode.Right != null) Nodes.add(QNode.Right);
} while (Nodes.peek() != null);
// process the queue until it's empty
// peeking for a null element is certainly faster (or as fast) as
// calling for the list's length over and over again
}
It’s pretty much the same thing.
2 comments
Michael Haren said on 2010-03-04
(note: I skipped essential things like error checking, etc. e.g. this assumes that the root node n isn’t null)
Michael Haren said on 2010-03-04
This is better known as a Breadth First Search, btw
http://en.wikipedia.org/wiki/Breadth-first_search
Comments closed
